ЗАДАЧИ ОГЭ С ЦИКЛАМИ (9 КЛАСС)
Задание 15. Короткий алгоритм в различных средах исполнения
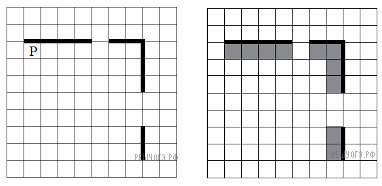
Задача 1. На бесконечном поле есть горизонтальная и вертикальная стены. Правый конец горизонтальной стены соединён с верхним концом вертикальной стены. Длины стен неизвестны. В каждой стене есть ровно один проход, точное место прохода и его ширина неизвестны. Робот находится в клетке, расположенной непосредственно под горизонтальной стеной у её левого конца. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно ниже горизонтальной стены и левее вертикальной стены. Проходы должны остаться незакрашенными. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).
При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для любого допустимого расположения стен и любого расположения и размера проходов внутри стен. Алгоритм может быть выполнен в среде формального исполнителя или записан в текстовом редакторе. Сохраните алгоритм в текстовом файле.
Решение: Следующий алгоритм выполнит требуемую задачу.
|
нц пока не сверху свободно
|
Задача 2. Напишите программу, которая в последовательности натуральных чисел определяет максимальное число, кратное 5. Программа получает на вход количество чисел в последовательности, а затем сами числа. В последовательности всегда имеется число, кратное 5. Количество чисел не превышает 1000. Введённые числа не превышают 30 000. Программа должна вывести одно число — максимальное число, кратное 5.
Пример работы программы:
| Входные данные | Выходные данные |
3 10 25 12 | 25 |
Решение: Следующий алгоритм выполнит требуемую задачу.
|
алг
|
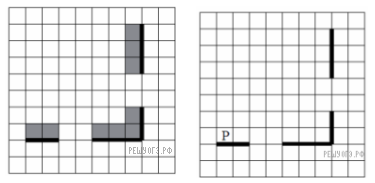
Задача 3. На бесконечном поле есть горизонтальная и вертикальная стены. Правый конец горизонтальной стены соединён с нижним концом вертикальной стены. Длины стен неизвестны. В каждой стене есть ровно один проход, точное место прохода и его ширина неизвестны. Робот находится в клетке, расположенной непосредственно над горизонтальной стеной у её левого конца. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно выше горизонтальной стены и левее вертикальной стены. Проходы должны остаться незакрашенными. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).
При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для любого допустимого расположения стен и любого расположения и размера проходов внутри стен. Алгоритм может быть выполнен в среде формального исполнителя или записан в текстовом редакторе. Сохраните алгоритм в текстовом файле.
Решение: Следующий алгоритм выполнит требуемую задачу.
|
нц
|
Задача 4.
Напишите программу, которая в последовательности натуральных чисел определяет сумму чисел, кратных 6. Программа получает на вход количество чисел в последовательности, а затем сами числа. В последовательности всегда имеется число, кратное 6. Количество чисел не превышает 100. Введённые числа не превышают 300. Программа должна вывести одно число — сумму чисел, кратных 6.
Пример работы программы:
| Входные данные | Выходные данные |
3 12 25 6 | 18 |
Решение: Следующий алгоритм выполнит требуемую задачу.
|
алг
|
Рассмотреть задачи ЕГЭ (11 класс) с циклами